This page is here to document some of the best practices to use when coding in Fortran. The main considerations in regard to on-node performance (at least on the CPU) could be categorized as: (1) threading, (2) caching, (3) memory accesses, (4) vectorization, (5) floating point issues, (6) accelerator porting issues, and (7) miscellaneous performance bugs.

Memory Accesses

Loop / Array ordering

It's best if the data is accessed in the same manner it's stored. Fortran uses column-major indexing, meaning the fastest varying index is always the innermost. Your innermost index should be the innermost loop in a nested loop. When the CPU requests an address from main memory, these accesses are very slow, and they never grab one datum at a time but rather a chunk of memory at a time. So having the next piece of data you're going to use in your loop be the next value in memory is a good thing.

Bad Example

do k = 1 , nz
  do j = 1 , ny
    do i = 1 , nx
      a(k,j,i) = b(k,j,i) + c(k,j,i)

Good Example

do k = 1 , nz
  do j = 1 , ny
    do i = 1 , nx
      a(i,j,k) = b(i,j,k) + c(i,j,k)

Indirect Addressing

There are many cases when one needs to use indirect addressing. The most common is when you have an unstructured mesh like we have in HOMME and MPAS-O, for instance. A couple of examples are:

do ie = 1 , nelems
  do i = 1 , num_neighbors
    elem(ie)%val = elem(ie)%val + elem(ie)%neighbor(i)%val2

do i = 1 , n
  packed(pindex(i)) = data(i)

The point is that you don't know a priori what memory you're going to access because it's being mapped in some way. These accesses could be random, strided, near, or far away. This type of access will perform quite bad by itself. The general solution to this is to have a dimension that is contiguous inside the indirect addressing so that the vast majority of accesses are still contiguous in memory. An example of padding with the vertical looping dimension is below:

do ie = 1 , nelems
  do i = 1 , num_neighbors
    do k = 1 , nlevels
      elem(ie)%val(k) = elem(ie)%val(k) + elem(ie)%neighbor(i)%val2(k)

do i = 1 , n
  do k = 1 , nlevels
    packed(k,pindex(i)) = data(k,i)

Repeated Array Accesses

There are many cases where you have inside a loop repeated accesses to the same index location of an array like the example below:

do j = 1 , np
  do l = 1 , np
    dat2(l,j) = 0
    do i = 1 , np
      dat2(l,j) = dat2(l,j) + matrix(i,l)*dat1(i,j)
    end do

Compilers often don't do that well with this kind of pattern because every time you access "dat2(l,j)", the compiler tends to try to access DRAM every single time, which is not very efficient. For sure, it's probably going to be in cache, but I've found compilers don't seem to this very efficiently. The best thing to do for repeated array accesses is to replace them with scalar temporary variables like the example below:

do j = 1 , np
  do l = 1 , np
    tmp = 0
    do i = 1 , np
      tmp = tmp + matrix(i,l)*dat1(i,j)
    end do
    dat2(l,j) = tmp

What this tends to do is "strongly encourage" the compiler to do the correct thing, namely place the variable "tmp" into register, which has no latency for access and is immediately available for the floating point unit to use.

Allocatable, pointer, target, aliasing, contiguous arrays

There is a good overview of the subject, accessible after you create an account: http://www.pgroup.com/lit/articles/insider/v6n3a4.htm .

Shortly, variables declared with 'allocatable' are assumed to be not aliasing, while variables declared by 'pointer' will be assumed aliasing. For optimization, if possible, use 'allocatable' instead of 'pointer'.

'Allocatable' arrays, fixed-size and deferred-shape arrays are contiguous. Pointers are not. If function uses a pointer as an argument that is a dummy assumed-shape array, a temporary contiguous array or other overheads can be created (avoidable with attribute 'contiguous').  

Seems to be only relevant to PGI: In functions, dummy assumed-size arguments like 'real :: x(:,:)' need to be stride-1 for the leftmost dimension (contiguous for the 1st dimension). Using pointers thus may create overheads. 

Array Layout

There are two things to consider when deciding on the layout of an array: cache and vectorization.

Modern CPU caches have line widths of 64 consecutive bytes (an array of 8 doubles), which is the size of a single read (Nvidia GPUs read 128 consecutive bytes). To maximize cache performance, you should use an entire line before it's thrown out (this can be hard to measure; but is easy for us to do), and you should help the cache predictor by accessing it in a linear fashion. This translates to the well known rule of laying out the memory so consecutive quantities in memory correspond to the fastest index of loops.

Vectorization is a little harder - it relies on uncoupled data which we are doing the same things with being layed out in the same way that our vectors are. The variables maintained by gauss points of different elements in Homme's dycore are good examples of this, as they are rarely dependent on each other. This suggests putting the element index last, as this allows direct reads from memory to vector registers. This can conflict with the cache locality requirement, especially when threading over elements or using MPI, so an alternative is "tile" or "stripe" our data with values from different elements (levels might also work).

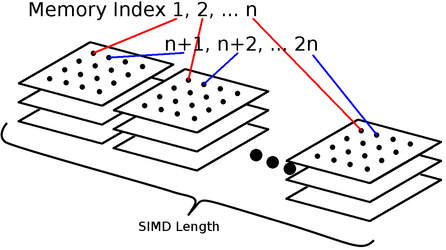
Vectorization

Vector units apply the same operation on multiple pieces of data at a time, or Single Instruction Multiple Data (SIMD). Using vector units is crucial for efficiency on all modern processors. If you want the compiler to automatically vectorize your loops, you need to make it easy for the compiler to know that the actions of that loop are indeed data parallel. The main inhibitors of vectorization for a loop are having a loop bound that isn't a simple integer, having a function call within the loop (that needs to be inlined), using print statements, and having if-statements. It's best for CPUs and KNLs if you can get if-statements out of the innermost loops altogether when possible. GPUs are actually very good at handling these by virtue of the fact that the moment you're on a GPU you're inherently already vectorized (the question now is just how efficiently).

There are cases when you'll have what's called a loop-carried dependence. The most common examples of this are reductions like the prefix sum or accumulation operation below:

do i = 1 , n
  array(i) = array(i-1) + dat1(i)**b
  dat2(i) = array(i)**c
enddo

This cannot do SIMD parallelism over the i-loop. The best solution for this is to precompute all of the main computations (like the exponentiation shown) into a temporary array in a SIMD manner, do the prefix sum in serial with as little work as possible, and then return to parallel work from there. This way the serial work is isolated to the least workload possible. This is shown below:

do i = 1 , n
  tmp(i) = dat1(i)**b
enddo
do i = 1 , n
  array(i) = array(i-1) + tmp(i)
enddo
do i = 1 , n
  dat2(i) = array(i)**c
enddo

What this will do is SIMD vectorize the first and third loops but not the center loop. But the center loop now has very little work to do in serial.

Whenever there is something that will inhibit vectorization, it's often best to fission the loop and isolate that operation by itself, and group the majority of the work together in loops that have work that all vectorizes.

Miscellaneous

Array Allocation

Modern languages can allocate memory for arrays in the "heap" and "stack".  Global arrays (arrays with the "save" attribute or arrays defined in a module outside of a subroutine) are allocated in the heap when the model initializes and these exist (taking up memory) for the entire simulation.  Arrays can be allocated while the code is running with the allocate() and deallocate() statements - these arrays are also placed in the heap, but the allocate() statement requires a system call and takes significant time (tens of thousands of instructions) as the system looks for available memory in the heap.  Allocate can be even slower when running in a threaded region - as it usually requires thread synchronization.  Allocate statement should never be used inside frequently called subroutines.  

Automatic arrays on the stack:  The most efficient way to create temporary arrays is to use local arrays declared in the subroutine.  These arrays will be placed on the stack (although sometimes compiler options are needed to force larger automatic arrays to be placed on the stack).  To create an array on the stack is nearly instant, as it just requires incrementing the stack pointer.   One drawback of stack variables is that each openMP thread must have it's own stack, and this memory must be allocated ahead of time, with the OMP_STACKSIZE environment variable.  Making this too small and the code will segfault when it runs out of stack memory, and making it too large, then allocating all this stacksize when the code starts can leave insufficient memory for the rest of the model.  

Stack arrays created inside a threaded region will be thread private.  Stack arrays created outside a threaded region can be shared by threads started later on in the subroutine, and marking such arrays "private" in openMP directives will create multiple copies of the array for each thread, which may or may not be what you want.  

Heap arrays are in the global memory space and accessible by all thread.  Sharing these arrays across threads requires synchronization if threads will be changing them independently.   Marking these arrays as private in an openMP directive should never be done. 

In C++, the stack and heap work the same as in Fortran; though it might be more difficult to tell when something uses the heap or the stack (I don't know enough Fortran to compare). Any data pointer initialized with 'malloc()' or 'new' (for C++, use new, as it will call constructors) will point to the heap. These should be deallocated with 'free()' or 'delete', respectively. C++ containers, such as list, vector, set, and map, will use the heap to store their data. Kokkos views will also be allocated on the heap unless initialized with a pointer to the stack. Note that initializing a view with a pointer to an array local to a kernel is broken in CUDA and should not be done.

Recommendation:

1. Allocate dynamic arrays only at a high level and infrequently
2. use stack arrays or for all subroutine array temporaries
3. understand the size of these arrays in order to have a good estimate of the needed stacksize
4. See below for similar problems with array slicing causing hidden allocation & array copies

Array Slicing

In my opinion, there are very few cases when array slicing is wise to do. I know it's a convenient feature of Fortran, but it's the cause of some of our worst performance degradations. The only time I think array slicing is OK is when you're moving a contiguous chunk of data, not computing things. For instance:

!Not wise because it's computing
a(:,i) = b(:,i) * c(:,i) + d(:)
g(:,i) = a(:,i) ** f(:)

!This is OK because it's moving a contiguous chunk of data
a(:,i) = b(:,i)

The problem is that when you have multiple successive array-slice notations, what this technically means is to put a loop around that one line by itself. For instance, the first two instructions above would translate into:

do ii = 1 , n
  a(ii,i) = b(ii,i) * c(ii,i) + d(ii)
enddo
do i = 1 , n
  g(ii,i) = a(ii,i) ** f(ii)
enddo

This is a problem because this would be more efficient if these two loops were fused together into the same loop because the value a(ii,i) is reused. However, as the code loops through the first loop, a(1,i) from the first iteration is likely already kicked out of cache by the time it's needed again by the second loop. Sometimes, compilers will automatically fuse these together, and sometimes they will not. To ensure they are performing well, you should have explicitly coded:

do ii = 1 , n
  a(ii,i) = b(ii,i) * c(ii,i) + d(ii)
  g(ii,i) = a(ii,i) ** f(ii)
enddo

Array Temporaries

But the potential caching problems of array slicing are nothing by comparison to the infamous "array temporary," which most Fortran compilers will tell you about explicitly when you turn debugging on. Take the following example for instance:

do j = 1 , n
  do i = 1 , n
    call my_subroutine( a(i,:,j) , b )

Because the array slice you passed to the subroutine is not contiguous, what the compiler internally does is create an "array temporary." The problem is that it nearly always allocates this array every time this function is called, copies the data, passes the allocated array to the subroutine, and deallocates afterward. It's the allocation during runtime for every iteration of that loop that degrades performance so badly. The best way to avoid this, again, is simply not to array slice. The better option is:

do j = 1 , n
  do i = 1 , n
	do k = 1 , n2
      tmp(k) = a(i,k,j)
    enddo
    call my_subroutine( tmp , b )

The reason this is more efficient is because you're not allocating "tmp" during runtime. Rather, you declare it as an automatic Fortran array, which most compilers have an option to place on the stack for efficiency.

Register Spilling

Register spilling occurs when the compiler can not keep all of the relevant local variables stored in registers, and must "spill" one or more onto the stack until needed again. To reduce register spilling, minimize the scope of variables and the distance between usage. Note this is also considered good code design as you're less likely to incorrectly use the variables in the code that doesn't need it (https://www.amazon.com/Code-Complete-Practical-Handbook-Construction/dp/0735619670/ref=pd_bxgy_14_img_3/134-1054583-1071544?_encoding=UTF8&psc=1&refRID=VT7CJN8DXPJ9EMTFRXY3).

! Don't do this
value = a + b ** 2 + c * d
... lots of code not using value ...
result = value + other_stuff


! Do this
... lots of code not using value ...
value = a + b ** 2 + c * d
result = value + other_stuff

Assembly

People familiar with assembly might consider inspecting the various versions produced by different compilers. A nice way to do that is to strip the code you're interested of external dependencies and put it through a tool like Compiler Explorer (note Compiler Explorer doesn't currently officially support Fortran, though according to this github issue you can enable it on GCC with the flag "-x f95"). Of course, reading the assembly can be misleading, so if it's not extremely obvious which is better, always measure!

Floating Point Issues

There are a couple of floating point issues to be aware of when coding. First, floating point division is far more expensive than floating point multiplication. What this means is that if you have a repeated division by a given value, you should compute the reciprocal of that value and multiply by the reciprocal inside loops. The exception to this is when you do this division fairly infrequently at different places in the code, in which case the likelihood of a cache miss outweighs the gain of multiplication being faster than division. For instance:

!Don't do this
do i = 1 , n
  a(i) = a(i) / b
enddo

!Do this instead
rb = 1. / b
do i = 1 , n
  a(i) = a(i) * rb
enddo

Also, floating point exponentiation is incredibly expensive (as are transendental functions). If you're computing the same exponentiation multiple times, you should replace them with a scalar constant to save on computation. Also, if you're exponentiating by an integer, make sure it's an integer! "a**2." consumes way more time than "a**2", which the compiler will likely recognize and change to "a*a".

FMA - Fused Multiply and Accumulate will compute a * x + b for the cost of a multiplication (on x86 AVX2 and CUDA), so structuring your code to take advantage of this will double the effective number of FLOPS you can get.

Accelerator Issues

Pushing Loops Down the Callstack

Accelerators need SIMD type parallelism exposed on scales much larger than those necessary for traditional CPUs. GPUs and MICs have different effective vector lengths, but for both, the vector length is long. This affects a lot of codes because most codes have routines that only work on a small amount of looping at a time. Our physics, for instance, in the atmosphere tend to do most of the work only over a single column at a time (i.e., 72 loop indices for current ACME hi-res). This is not enough to fill a vector unit on a GPU.

The solution for this is to push the loop across columns down into those routines so that the loop over vertical levels can be exposed in combination with the loop across columns to allow for much larger vector lengths. It's even better if you break off a "chunk" of columns and pass that down the callstack, and the user can define the size of the chunk at compile time. The reason this is better is that it allows flexibility in the effective vector length size as well as caching concerns. You could pass a chunk of "1" or a chunk of "256," for instance. Also, if this looping can all be exposed at the same time in a tightly nested manner, that would be preferable.

Modern Fortran

There are many features in modern Fortran that are not well supported (or supported at all) by OpenACC and OpenMP directives-based standards. In fact, CUDA doesn't support some of these features either. If you plan to use Modern Fortran in your code, you need to use it as a high-level wrapper only. The actual computation of your code needs to look like flat arrays or easy data structures if you expect to port it to GPUs or KNLs efficiently with directives-based approaches. Also, I've seen many cases where people write functions that define other functions in Fortran. Things like this should not be done. Rather, hoist the nested functions out to the module level.

Threading

Common Blocks, module use, and "save" attribute

The problem with common blocks, "use"ing data from modules, and using the "save" attribute is that each of these lead to data that is default shared between OpenMP threads. The only way to give each thread their own copy of data in any of these modes is to explicitly declare "!$omp threadprivate(var1,var2,...)". The exception to this is when a common block is used, in which case, one can mention "!$omp threadprivate(/common_block_name/)". But this is a tedious and often error-prone thing to do, and it is best if it can be minimized or avoided altogether.

First Touch

Often times, data will be initialized by a single thread or outside a threaded region while the typical accesses to that data are performed in a threaded manner. The problem with this is that a data's affinity to a thread (usually a core as well) is typically defined by first touch. You can fix this by initializing your data with the same threads you use for the calculations later.

Other threading recommendations:  

1. Minimize entrances and exits to parallel regions. OMP_WAIT_POLICY=ACTIVE can get around this, but it's more robust to make parallel regions as long as possible.  A caveat to this recommendation is that placing parallel regions very high in the call stack can create a large memory footprint (replication of temps, etc.) and can obscure the fact that developers are coding within a parallel region, resulting in errors. Using OMP PARALLEL DO around every loop creates too many entry/exits, but placing OMP PARALLEL around the entire time step loop results in large memory use and fragile code development. Somewhere in between these extremes is optimal and requires some experimentation.
2. Thread over nested loops using the collapse clause or explicit division-mod arithmetic (x86 computes integer division and mod in the same instruction, so this looks more expensive than it is).